图论基础知识总结及相关应用实践
Posted on 2022.03.27 by Zhang Pengwei under CC BY-SA 4.0
图结构基础知识的学习&复习范围(路径)如下:
- 基本概念:
- 图(graph)、子图(subgraph)、顶点(vertex)、边或弧(edge / arc)、权(weight)
- 有向无向(directed / undirected)、环(cycle)
- 联通非联通(connect / disconnected)、连通分量(connected component)
- etc.
- 存储结构及基本操作:
- 邻接矩阵(二维数组)、邻接表(adjacency list)
- 十字链表(orthogonal list)、邻接多重表(adjacency multilist)
- 遍历算法:
- 深度优先搜索
- 广度优先搜索
- 图的应用:
- 连通性问题 ~最小生成树
- Prim算法、Kruskal算法
- 有向无环图 ~拓扑排序 ~关键路径
- 最短路径问题
- Dijkstra算法、Floyd算法
- 连通性问题 ~最小生成树
图的存储结构及实现
邻接矩阵、邻接表是图的两种基本存储结构。
邻接矩阵直接用二维数组实现即可,在N*N的二维数组中,用Array[I][J]存储I点与J点的关系,可以用01表示有无关系,或用数字表示权值等。无向图的邻接矩阵是一个对称矩阵。
邻接矩阵存储稀疏图 浪费空间,由此引入邻接表。邻接表逻辑上由顶点表与边表构成,顶点表存储所有顶点,每个顶点对应一张边表,存储依附于该顶点的边。
以下基于邻接表实现一个基本的图结构:
class Vertex:
"""
顶点表元素,其中直接用self.edge存储对应边表
"""
def __init__(self, key: str):
self.key = key
self.edge = {} # 边表字典,key=所指向的节点id,value=权重
def addNeighbor(self, key, cost):
self.edge[key] = cost
def __str__(self):
desc = ''
if len(self.edge) > 0:
for edge in self.edge.items():
desc += f'({self.key}, {edge[0]}, {edge[1]})\n'
desc = desc[:-1] # 去除多余的换行
else:
desc = f'({self.key}, -, -)'
return desc
class Graph:
def __init__(self):
self.vertexList = {}
def insert_vertex(self, ver_id: str):
"""插入顶点"""
self.vertexList[ver_id] = Vertex(ver_id)
def add_edge(self, a, b, cost=0):
"""在a、b两节点之间添加一条边,默认无权重"""
a, b = str(a), str(b)
if a not in self.vertexList:
print(f'{a} not found, add vertex first please')
return
if b not in self.vertexList:
print(f'{b} not found, add vertex first please')
return
ver = self.vertexList.get(a)
ver.addNeighbor(b, cost)
def delete_vertex(self, v_id: int):
"""根据id号删除顶点"""
pass
def remove_edge(self, a, b):
"""移除a、b两节点之间的边"""
pass
def print_graph(self):
"""打印所有节点及节点间关系"""
for ver in self.vertexList.values():
print(ver)
if __name__ == '__main__':
g = Graph()
for i in range(5):
g.insert_vertex(str(i))
g.add_edge(1, 2, 99)
g.add_edge(1, 3, 88)
g.add_edge(1, 4, 77)
g.add_edge(2, 4, 66)
g.print_graph()
"""output
(0, -, -)
(1, 2, 99 )
(1, 3, 88 )
(1, 4, 77 )
(2, 4, 66 )
(3, -, -)
(4, -, -)
"""
除了上述两种存储结构,按照严版数据结构,还有邻接多重表、十字链表等,都是在上述基础上的优化变种,看具体应用场景灵活实现就好。
图的遍历
图的遍历即【从某顶点出发不重复地访问图中所有顶点】,是各种相关算法的基础,主要有两种基本方法:
- 广度优先搜索(breadth first search,简称BFS)
- 深度优先搜索(depth first search,简称DFS)
BFS
BFS可类比二叉树的层序遍历,需要一个队列存储本层所访问的节点,方便进行下一层的处理。注意图不像二叉树按序遍历就可以实现每个节点的唯一访问,图中不同节点相互关联,访问时需要标记每个节点是否被访问过。
算法思路:
- 对每个连通分量分别处理
- 访问顶点,入队列
- 从队列取出一个顶点,访问其所有邻接顶点
- 将每个访问过的顶点依次入队列
- 重复上述过程,直到队空
代码实现:
from graph import Graph
from graph import Vertex
def bfs(g: Graph):
"""breadth first search 图的广度优先搜索"""
all_vertex = g.get_all_vertex() # 顶点表 list[Vertex,Vertex,Vertex,,,]
is_visited = {} # 标记顶点是否被访问过,key=顶点id,value=1为被访问过
ver_queue = []
print('BFS -> ', end='')
for vertex in all_vertex: # 外层循环:遍历所有联通分量
# print('try new component' + '_' * 20)
if vertex.key not in is_visited.keys():
# 处理联通分量第一个顶点,初始化队列
print(vertex.key + ' -> ', end='')
is_visited[vertex.key] = 1
ver_queue.append(vertex)
# 中层循环:遍历该联通分量
while len(ver_queue) > 0:
cur = ver_queue.pop(0) # 当前处理的顶点
# 内层循环:遍历某顶点所有邻接顶点
for vertex_ in cur.get_all_neighbor():
if is_visited.get(vertex_) is None:
# 访问过后将该顶点入队列,等待后续访问其相邻节点
# 由于此处vertex_是字符串,队列里需要存入Vertex类
# 前面构造Vertex类的时候图省事,此处只好再从g中取下
print(vertex_ + ' -> ', end='')
is_visited[vertex_] = 1
ver_queue.append(g.get_vertex(key=vertex_))
print('END')
if __name__ == '__main__':
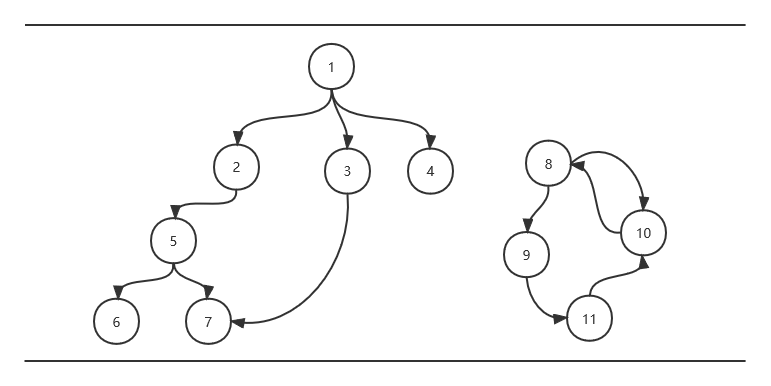
"""对题图进行测试,后续构造过程与此相同不再重复"""
g = Graph()
for i in range(1, 12):
g.insert_vertex(str(i))
g.add_edge(1, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
g.add_edge(2, 5)
g.add_edge(5, 6)
g.add_edge(5, 7)
g.add_edge(3, 7)
g.add_edge(8, 9)
g.add_edge(8, 10)
g.add_edge(9, 11)
g.add_edge(11, 10)
g.add_edge(10, 8)
bfs(g)
# BFS -> 1 -> 2 -> 3 -> 4 -> 5 -> 7 -> 6 -> 8 -> 9 -> 10 -> 11 -> END
DFS
DFS可类比二叉树的先根序遍历, 沿着一条路径向下访问,直到走到“叶子”节点(不再有未访问的邻接顶点),向上回溯,重复这个过程直到所有顶点都被遍历。
算法思路:
- 对每个连通分量分别处理
- 有未访问的邻接顶点,则取一个向下探索
- 走到叶子节点了,向上回溯,重复步骤1
- 重复上述过程直到所有节点遍历完毕
代码实现(递归):
from graph import Graph
from graph import Vertex
def dfs(g: Graph):
"""depth first search 图的深度优先搜索"""
all_vertex = g.get_all_vertex()
# 换个写法记录是否被访问过,列表坐标作为key标记对应顶点
# 这样做的前提是,顶点的key是int类型的(或可兼容的)
is_visited = [False for _ in range(len(all_vertex) + 1)]
def dfs_recursive(v: Vertex):
print(v.key + ' -> ', end='') # 访问
is_visited[int(v.key)] = True # 标记
for vertex_ in v.get_all_neighbor():
if not is_visited[int(vertex_)]:
dfs_recursive(g.get_vertex(vertex_)) # 递归向下遍历
print('DFS_Recur -> ', end='')
for vertex in all_vertex:
if not is_visited[int(vertex.key)]:
dfs_recursive(vertex)
print('END')
# DFS_Recur -> 1 -> 2 -> 5 -> 6 -> 7 -> 3 -> 4 -> 8 -> 9 -> 11 -> 10 -> END
递归转非递归,人工建栈模拟系统的自动压栈出栈。
代码实现(非递归):
from graph import Graph
from graph import Vertex
def dfs_unrecursive(g: Graph):
"""depth first search 图的深度优先搜索 非递归实现"""
# 注意对比以下非递归实现与BFS的细微区别(queue vs stack)
all_vertex = g.get_all_vertex()
is_instack = [False for _ in range(len(all_vertex) + 1)]
ver_stack = []
print('DFS_unRecur -> ', end='')
for vertex in all_vertex:
if not is_instack[int(vertex.key)]:
is_instack[int(vertex.key)] = True # 标记
ver_stack.append(vertex)
while len(ver_stack) > 0:
vertex_ = ver_stack.pop()
# pop不传参则默认处理最后一个元素 (index = -1)
# print('visit ' + vertex_.key)
print(vertex_.key + ' -> ', end='')
for v_str in vertex_.get_all_neighbor():
if not is_instack[int(v_str)]:
ver_stack.append(g.get_vertex(v_str))
is_instack[int(v_str)] = True # 标记
print('END')
# DFS_unRecur -> 1 -> 4 -> 3 -> 7 -> 2 -> 5 -> 6 -> 8 -> 10 -> 9 -> 11 -> END